비리얼 정리에 대해 찾아보니 정확하게 나와 있지 않은 것 같아서 쓰는 글이다.
아마 임용고시를 준비하는 사람들이나 과학고 학생들이 보게될 것 같다.
이 글을 알기 전에 역학적 에너지와 포텐셜 에너지, 그리고 원운동을 물리적으로 어떻게 서술하는지를 알고 읽도록 하자.
이번 글에서는 비리얼 정리에 대해 알아보고, 다음 글에서는 비리얼 정리를 통한 은하의 질량 추정에 대해 알아보고자 한다.
1. 비리얼 정리
비리얼 정리는 무질서하게 움직이는 여러 입자들 사이의 힘에 대하여 서술하는 정리이다.
천문학에서 비리얼 정리를 이용하는 것은 항성의 형성, 은하의 형성이 하나의 질점에서 이루어지는 것이 아니라 불규칙하게 움직이는 여러 질점의 합으로 이루어지기 때문이다.

천문학에서 비리얼 정리는 입자들의 운동량과 방향을 모두 더한 값이다.
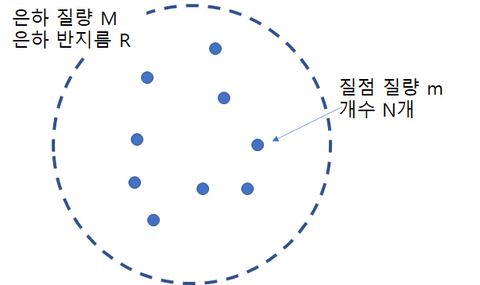
예를들어 위의 그림과 같이 별이 3개뿐인 은하가 있다.
이 은하 안에서 움직이는 모든 천체의 운동량과 방향의 곱을 합하면 된다. 이 은하에서의 비리얼 정리를 구한다면 아래와 같을 것이다.

위의 값을 그대로 보았을 때는 이해하기 어렵지만, 시간에 따른 비리얼 값의 변화를 보면 이것이 어떤 의미를 가지는지 알게 된다.
그러기 위해서 운동량과 방향의 곱을 미분하면 어떤 의미를 가지는지 먼저 알아보고 넘어가보자. 아래와 같이 먼저 수식을 정의하겠다.
물체의 질량 = m, 속도 = v
가속도 = a, 운동량 = p = m * v
중력 = F
dp/dt(시간에 따른 운동량 변화) = ma = F거리와 운동량의 곱을 시간에 대해서 미분하면 아래와 같은 식을 얻게 된다.

여기서 시간에 따른 운동량의 변화는 힘이고, 시간에 따른 거리의 변화는 속도이므로 이 식은 아래와 같이 바뀔 수 있다.

결국 운동량과 방향의 곱을 시간에 대해 미분 하면 어떤 물체가 가진 역학적 에너지의 합이 나온다.
마찬가지로 비리얼 값을 시간에 대해 미분하면 어떤 계가 가진 역학적 에너지의 합이 나오는 것이다.
그 값은 계가 가진 위치 에너지와 운동에너지의 2배를 합한 것과 같다.

위의 은하에서 비리얼 정리를 하고 이를 시간에 따라 미분 한다면 별A, B, C 가 가진 역학적 에너지의 합이 나오게 된다.
은하나 성운이 안정되고 평형을 이루고 있는 상태라면 역학적 에너지의 변화는 없어야 한다.
따라서 비리얼 값의 변화량도 0이어야 한다.

역학적으로 안정되고 평형을 이루고 있는 은하와 성운이라면, 내부에서 가지는 역학적 에너지의 총량은 위치 에너지 총량의 반이라는 것이다.
이것을 통해 어떤 은하나 가스 성운의 크기와 속도분산, 온도만 알고 있다면 질량을 구할 수 있게 된다.
2. 불안정한 계에서의 비리얼 정리
계가 안정된 상태가 아니라면 비리얼은 계속 변하게 될 것이다.
비리얼 값이 감소한다면 계는 수축하게 될 것이고, 비리얼 값이 증가한다면 계는 팽창하게 될 것이다.
이를 활용하면 별이 만들어 질 때 수축 가능한 최대 질량을 구할 수 있다.

3. 고등학교 물리로 이해하는 비리얼 정리
그럼 이제 고등학교 수준에서 이 수식을 어떻게 간단하게 이해할 수 있는지 보자.
천체들은 서로 중력에 의해 구속되고 있다.
비리얼 정리는 서로 구속되어 있는 모든 천체의 적분이지만, 결국에는 하나의 천체에 있는 역학적 에너지들의 합과 같다.
따라서 하나의 천체에 대해서 역학적 에너지가 어떻게 구해지는지 보려고 한다.

위와 같이 지구 주변에 공전하는 질량m 인 천체를 가정해보았다.
천체는 지구 주변을 공전한다.
이때 천체의 역학적 에너지는 아래와 같다.

이때 원운동의 속도를 구해보자.
원운동은 만유인력에 의해서 일어나므로 구심력과 만유인력은 같아야 한다.
이를 속도에 대해 정리하면

이와 같은 수식을 얻을 수 있다.
이것을 처음에 기술했던 천체의 역학 에너지에다 집어넣어 보자! 그럼....

위와 같은 결론이 나온다.
결국 중력적으로 속박된 계에서 운동에너지의 총 합은 위치에너지의 절반이 되는 것이다.
이는 위에서 비리얼 정리를 통해 얻은 결론과 똑같다.

중요한 것은 이것을 이용하여 어떻게 천체의 질량을 추정할 수 있는가이다.
이것은 다음 게시물에서 다루겠다.
4. 비리얼 정리와 복사 방출
지구에서 아주 멀리 있는 천체가 지구쪽으로 접근하여 결국 지구로 속박되게 되었다면 계가 가진 에너지의 총량은 어떻게 될까?
처음에 물체가 정지 상태였다고 가정한다면, 계가 가진 에너지의 총량은 0이었을 것이다.

그런데 이 천체가중력적으로 끌려 들어와 지구 주변을 돌게 된다면 위치 에너지가 감소하여 운동에너지로 전환될 것이다.

이 경우에 계가 '안정된' 상태라고 가정하고 역학적 에너지의 총량을 구해보면 신기하게 처음보다 에너지가 감소한다.

구속된 천체의 포텐셜 에너지의 반만큼이 사라진 것이다.
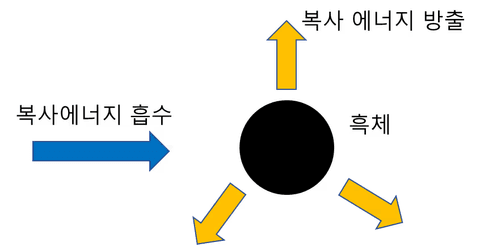
사라진 에너지는 열로 전환된다.
우주가 진공상태이기 때문에 전도, 대류를 통해서는 계에 에너지가 계속 남아있으므로 소실이 없다.
하지만 복사는 이에 대해 자유롭기 때문에 우주 공간으로 빠져나갈 수 있다.
따라서 안정된 계라면 이 만큼의 에너지는 '복사방출'을 통해서 계를 떠나야 한다는 결론이다.
5. 결론 : 비리얼 정리란 무엇인가?
1) 비리얼 정리란 천체 내부 질점의 운동량과 방향을 모두 더한 값이다.
2) 시간에 따른 비리얼 값의 변화는 천체의 안정도를 결정해준다.
3) 안정되고 평형을 이룬 천체 내에서의 비리얼 값의 변화는 없으며, 이를 이용하면 천체의 질량을 추정할 수 있다.다음 시간에는 3)을 활용한 천체의 질량을 추정하는 방법에 대해 알아보려고 한다. 계속해서 글을 읽고자 하는 사람은 아래의 링크로 접속하기 바란다.





댓글을 불러오는 중...