教師のための教育研究および統計分析研修 - 第7回 単回帰モデル：切片と傾き

今日の研究質問はやや独特である。

アイスクリーム販売量と溺死事故者数との関係はどのようになっているだろうか？

仮想データが下記の通りだとしよう。

これについて回帰直線を描くと、次のようになる。

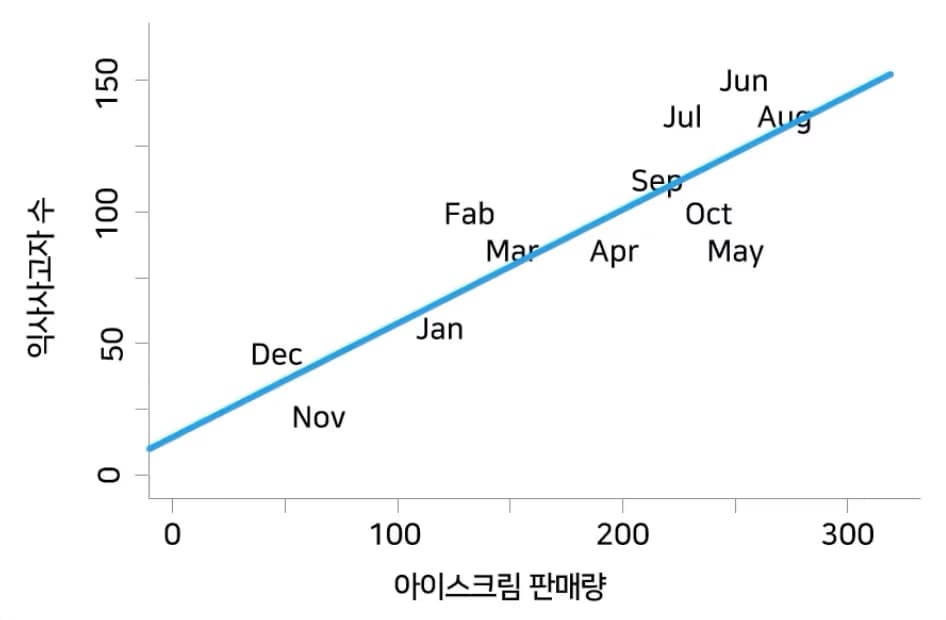
ここで、傾き・切片はどのような意味を持つだろうか。

1. 良い回帰直線と悪い回帰直線

回帰分析のグラフを推定するときは、どのようにすればよいのだろうか。

もちろん、目で見てどのグラフがデータをよりよく説明しているか直感的に説明することはできるが、論文を準備するのであれば、これを数学的に表現できなければならない。

このとき、残差（residual）というものを用いる。

残差 = 実測値 - 予測値 である。

残差が小さいほど、良い回帰直線だと言える。

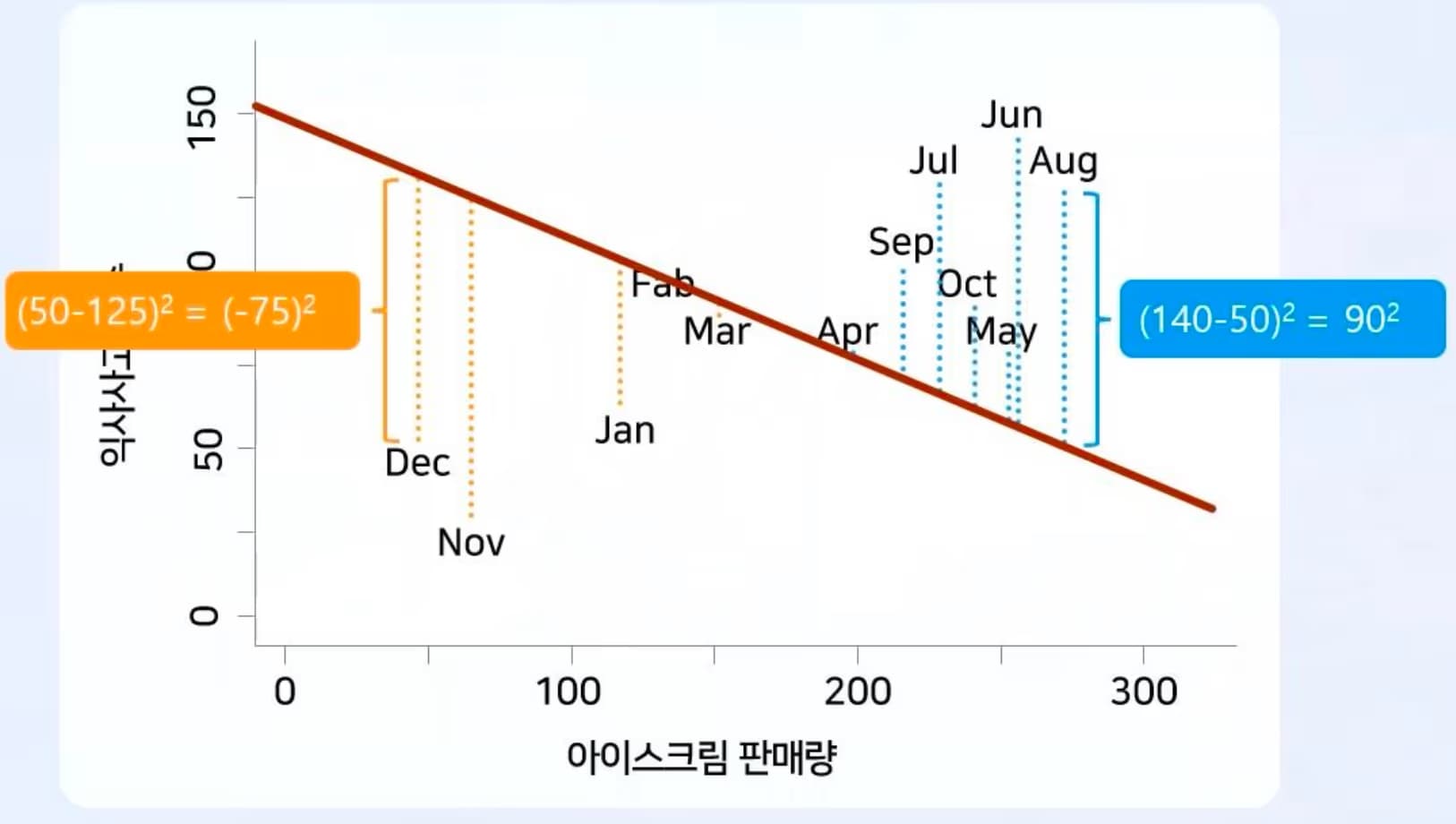
しかし、残差を単純に足し合わせると問題が生じる。

残差は正の場合もあれば負の場合もあるからである。

そこで、残差を二乗した最小二乗和というものを求める。

これによって回帰直線の適合性を分析することができる。

2. 線形回帰分析

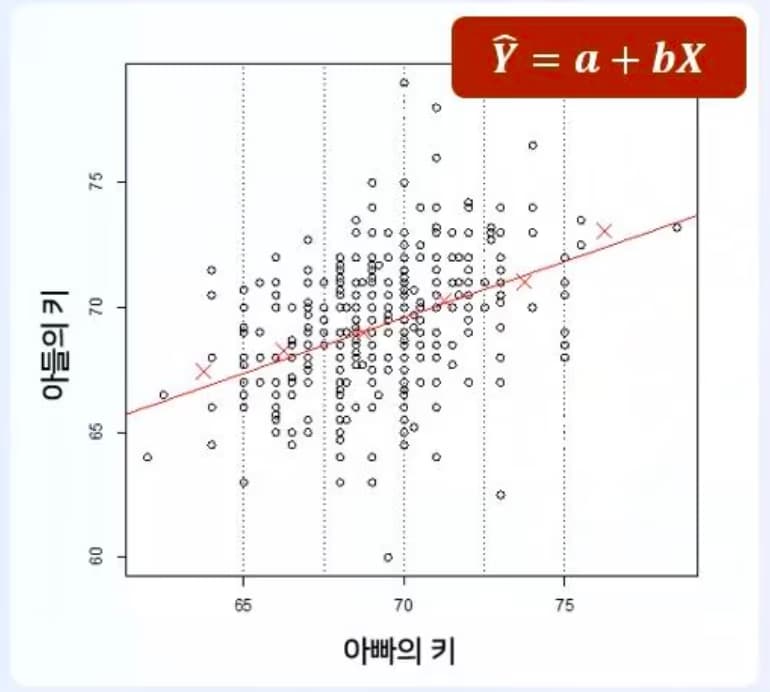
変数間の関連性を直線で要約したものである。

回帰直線を求める過程とは、切片と傾きを求めていく過程である。

線形回帰分析とは、最小二乗和が最も小さくなるような切片と傾きを求めることでもある。

3. 後記

回帰直線を評価するときに、最小二乗和というものを用いるという発想自体がとても新鮮だった。

「回帰直線がデータと似ていればそれで良いだろう」と単純に考えていたのとは違い、それを数学的に定義し、それを理解しておかなければならないという点が新しく感じられた。

そして、その定義自体も難しくはなかった。

今日もひとつ学んで帰る。