La pregunta de investigación de hoy es algo peculiar.
¿Qué relación habrá entre la cantidad de helados vendidos y el número de personas ahogadas?Supongamos que los datos ficticios son como los de abajo.
Si trazamos la recta de regresión para esto, se verá como sigue.
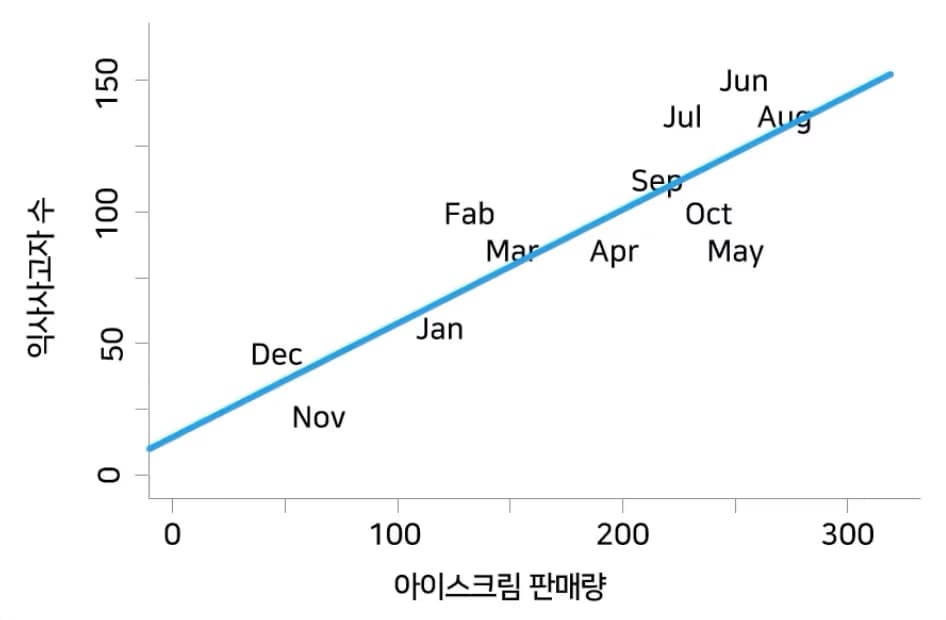
¿Qué significado tienen aquí la pendiente y el intercepto?
1. Buena recta de regresión y mala recta de regresión
Cuando estimamos el gráfico de un análisis de regresión, ¿cómo debemos hacerlo?
Por supuesto, a simple vista podemos explicar de manera intuitiva qué gráfico describe mejor los datos, pero si estamos preparando un artículo es necesario poder expresarlo matemáticamente.
En ese momento se utiliza lo que se llama residuo (residual).
Residuo = valor real - valor predicho.
Cuanto más pequeño es el residuo, mejor es la recta de regresión.
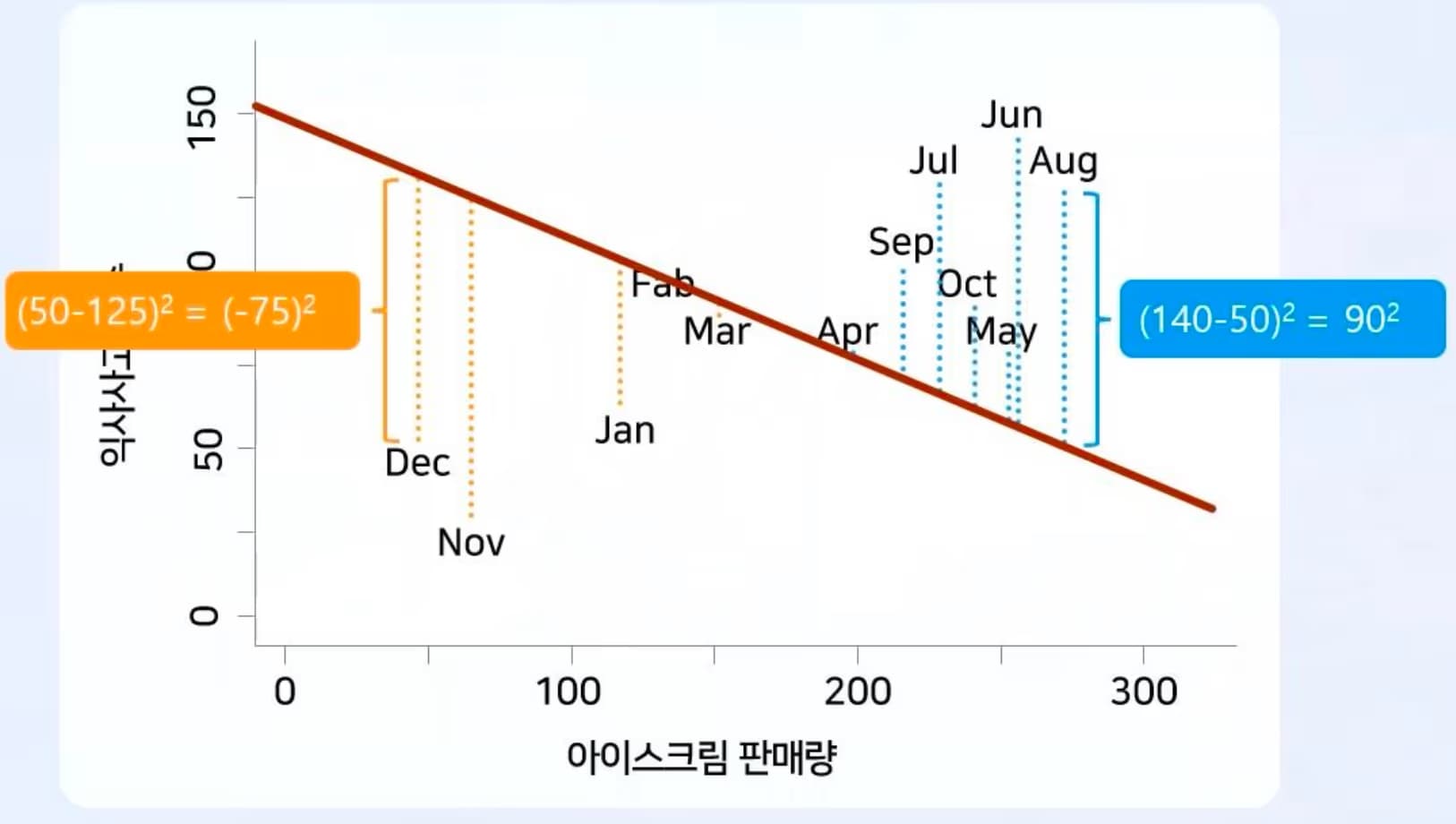
Sin embargo, simplemente sumar los residuos genera problemas.
Esto se debe a que los residuos pueden ser positivos, pero también negativos.
Por ello se calcula lo que se llama la suma de cuadrados mínimos de los residuos.
Con esto se puede analizar el grado de ajuste de la recta de regresión.
2. Análisis de regresión lineal
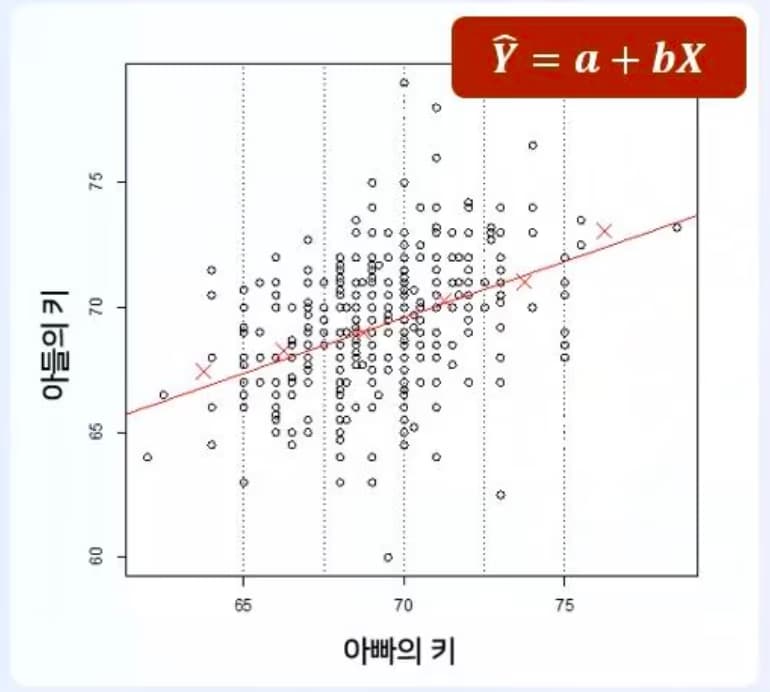
Es un método que resume la relación entre variables mediante una línea recta.
El proceso de hallar la recta de regresión es el proceso de encontrar el intercepto y la pendiente.
El análisis de regresión lineal también consiste en encontrar el intercepto y la pendiente que hagan mínima la suma de cuadrados mínimos.
3. Comentario final
Me resultó muy novedoso el propio hecho de que, al evaluar una recta de regresión, se utilice algo llamado suma de cuadrados mínimos.
A diferencia de cuando pensaba de forma sencilla que “si la recta de regresión se parece a los datos, entonces es buena”, me llamó la atención que haya que definir esto matemáticamente y entenderlo.
Y la definición en sí no era difícil.
Hoy también me voy habiendo aprendido algo nuevo.






댓글을 불러오는 중...