查找比里尔定理时,似乎没有准确的解释,因此写下这篇文章。
可能会被准备教师资格考试的人或科学高中的学生看到。
在了解本文之前,请先了解如何物理地描述机械能、势能和圆周运动。
本文将了解比里尔定理,下一篇文章将探讨通过比里尔定理估算银河的质量。
1. 比里尔定理
比里尔定理是描述多颗无序移动的粒子之间力的定理。
在天文学中利用比里尔定理是因为恒星的形成、星系的形成不是由一个质点组成的,而是由多个不规则移动的质点的总和组成的。

在天文学中,比里尔定理是所有颗粒动量和方向的总和。
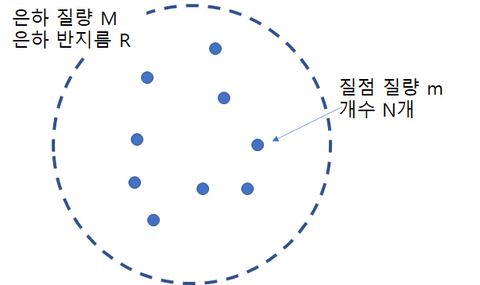
例如,如上图所示,有一个只有3颗星的星系。
在这个星系中移动的所有天体的动量和方向的乘积即可。要在该星系中应用比里尔定理,则为如下。

从上述数值直接看很难理解,但看到随时间变化的比里尔数值时,就能明白其意义。
为此,我们先了解动量與方向的乘积对时间微分的意义。如下先定义公式。
物体的质量 = m, 速度 = v
加速度 = a, 动量 = p = m * v
重力 = F
dp/dt(动量的时间变化) = ma = F距离和动量的乘积随时间的微分,即可得到如下公式。

这里,动量的时间变化是力,距离的时间变化是速度,因此此公式可改为如下。

最终,动量和方向的乘积对时间的微分,会得出物体所拥有的机械能之和。
同样,比里尔值对时间的微分,会得出系统所拥有的机械能之和。
该数值是系统所拥有的位置能和动能的2倍之和。

若对上面的星系应用比里尔定理并对其随时间微分,则会得出恒星A、B、C拥有的机械能之和。
假如银河或星云处于稳定和平衡状态,则机械能的变化应为0。
因此,比里尔值的变化量也应为0。

力学上稳定和平衡的银河及星云内部所拥有的机械能的总和是位置能总量的一半。
通过此,可以通过已知银河或气体星云的规模、速度分散、温度来计算其质量。
2. 不稳定系统中的比里尔定理
若系统不在稳定状态,比里尔将不断变化。
比里尔值减少则系统会收缩,比里尔值增加则系统会膨胀。
利用此可计算恒星形成时可收缩的最大质量。

3. 用高中物理理解比里尔定理
现在让我们看看如何在高中水平上简单地理解此公式。
天体间受到重力束缚。
比里尔定理是被束缚的所有天体的积分,但最终相当于一个天体的机械能之和。
因此,我们试图了解单个天体的机械能是如何计算的。

如上图所示,假设一个质量为m的天体绕地球公转。
天体绕地球公转。
此时天体的机械能如下。

接下来计算圆周运动的速度。
圆周运动是由于万有引力发生的,因此向心力和万有引力应相等。
将其整理为关于速度的公式,则

可得出这样的公式。
将此代入之前描述的天体机械能!然后....

得出如上的结论。
在引力封闭系统中,运动能的总和是位置能的一半。
这与通过比里尔定理得出的结论相同。

重要的是如何利用此来估算天体的质量。
这将在下一篇文章中讨论。
4. 比里尔定理与辐射发射
从地球很远的天体接近地球,最终被地球捕获,系统所拥有的能量总和将如何变化?
假设物体最初是静止的,那么系统所拥有的能量总和应为0。

但是,该天体被引力吸引到地球附近时,位置能减少并转化为动能。

在假设系统为'稳定状态'时计算机械能的总和,惊人的是比最初能量减少。

被束缚的天体潜能的一半消失。
消失的能量转化为热。
由于宇宙处于真空状态,通过导电、对流,能量在系统中保持,不会消失。
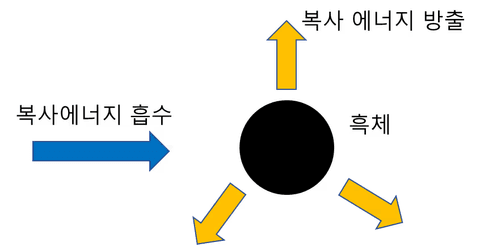
但辐射对此自由,能量可以跑到宇宙空间中。
因此,对于稳定系统,该能量应通过'辐射发射'离开系统。
5. 结论:比里尔定理是什么?
1) 比里尔定理是天体内部质点的动量和方向的总和。
2) 随时间变化的比里尔值决定天体的稳定性。
3) 平衡且稳定的天体内比里尔值的变化为零,可以用来估算天体的质量。下一次将探索如何利用3)来估算天体的质量。想继续阅读的读者请访问以下链接。





댓글을 불러오는 중...