오늘의 연구 질문은 다소 독특하다.
아이스크림 판매량과 익사사고자 수 간의 관계는 어떨까?가상의 데이터가 아래와 같다고 하자.
여기에 대해 회귀선을 그리면 아래와 같다.
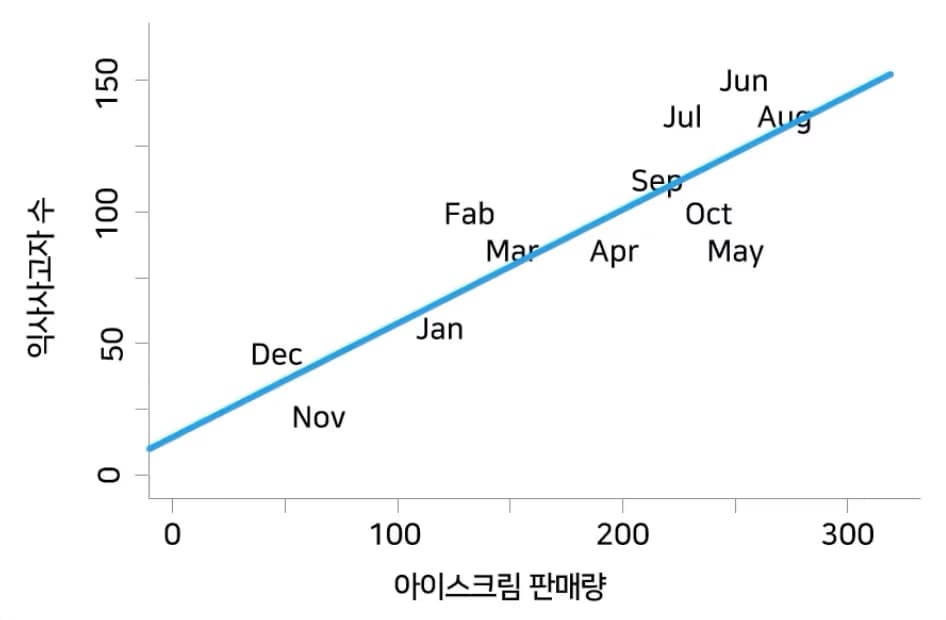
여기에서 기울기, 절편은 어떤 의미를 가질까?
1. 좋은 회귀선과 나쁜 회귀선
회귀분석의 그래프를 추정할 때는 어떻게 해야할까?
당연히 눈으로 보았을 때 어떤 그래프가 더 자료를 잘 설명하는지 직관적으로 설명할 수 있지만, 논문을 준비한다면 이것을 수학적으로 표현할 수 있어야 한다.
이때 잔차(residual)이라는 것을 이용한다.
잔차 = 실제값 - 예측값 이다.
잔차가 작을수록 좋은 회귀선이라고 할 수 있다.
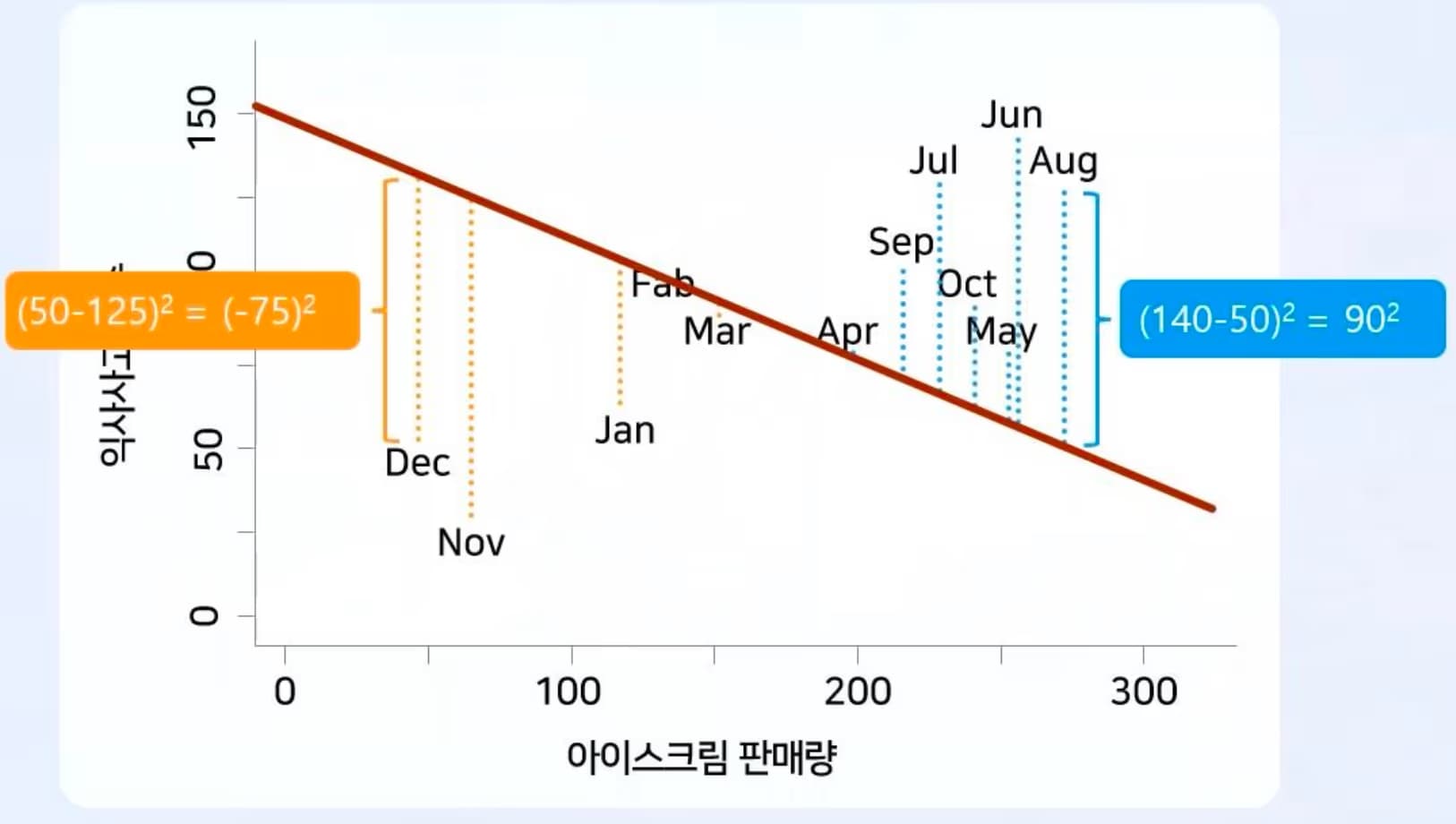
하지만 잔차를 단순히 더하는 것은 문제가 발생한다.
잔차가 양수일수도 있지만, 음수도 있기 때문이다.
이에 잔차를 제곱하는 최소자승합이라는 것을 구한다.
이것으로 휘귀선의 적합성을 분석할 수 있다.
2. 선형회귀분석
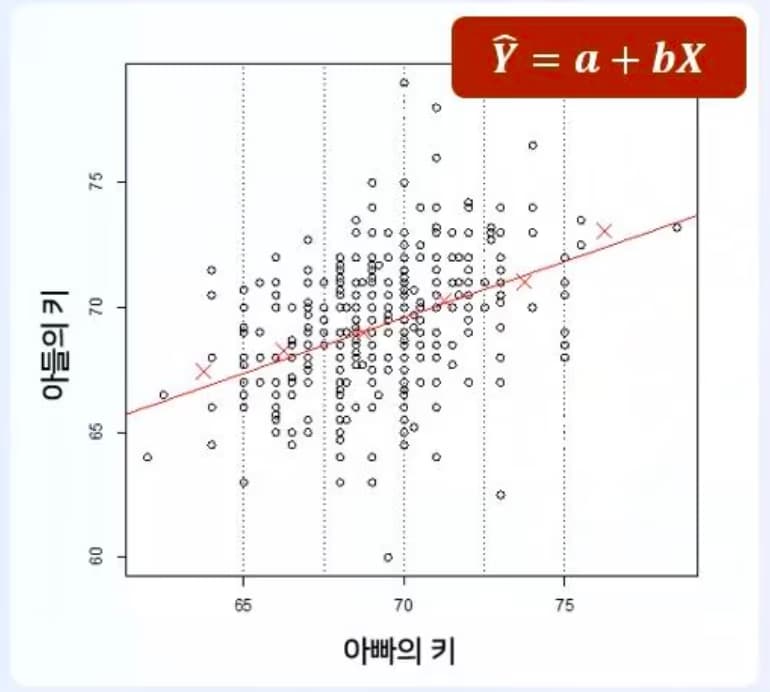
변수들 간의 관련성을 직선으로 요약한 것이다.
회귀선을 찾아내는 과정은 절편과 기울기를 찾아가는 과정이다.
선형회귀분석 또한, 최소자승합이 가장 작도록 하는 절편과 기울기를 구하는 것.
3. 후기
회귀선을 평가할 때, 최소자승합이라는 것을 이용한다는 생각 자체가 무척 신선했다.
그냥 회귀선이 자료랑 비슷하면 그게 좋은거지라고 단순하게 생각했던 것과 달리, 이것을 수학적으로 정의해하고 그걸 알아야 한다는게 새롭게 다가왔다.
그리고 정의 자체도 어렵지 않았다.
오늘도 하나 배우고 간다.






댓글을 불러오는 중...