光学的深さに続いて伝達方程式について学びたい。
もしまだ光学的深さが何かよくわからないなら、以下の文を読んでからこの文を読んでほしい。
1. 伝達方程式の定性的思考
伝達方程式は、ある天体内部で光が伝達される過程を示したものである。
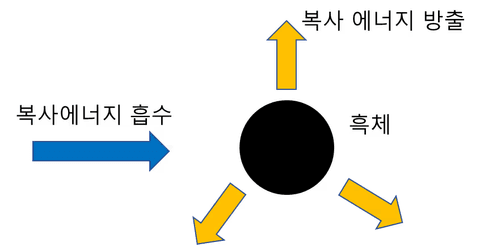
一般的に天体は光を吸収したり、同時に放出したりもする。教室に例えて話してみよう。
1) 生徒たちが前の先生(観測者)にコインを順番に渡す。
2) 各生徒は後ろからコインを受け取ったら、その中の1個を持って(消光)4個を追加(放出)する。
3) 先生はいくつのコインを受け取ることができるのか?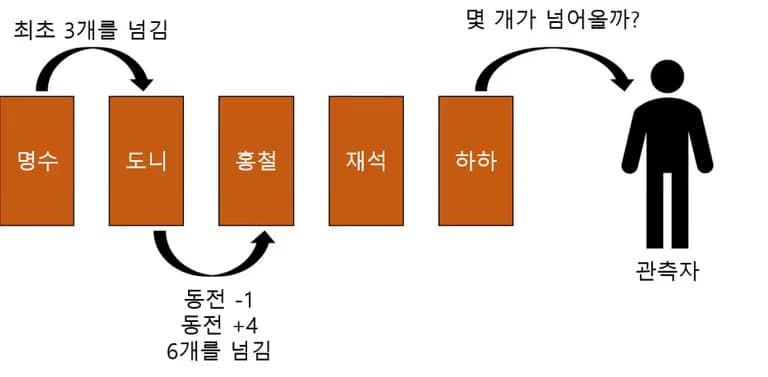
それでは、それぞれの生徒を通過するたびに コインの変化量はコインの追加量(放出量)- コインを持つ量(消光)と同じになる。
そして コインの追加の程度は通過する人数が多いほど(通過する長さが増えるほど)増大する。
通過する長さが長ければ長いほど、 最初にメンスが渡したお金はすべて生徒が持ってしまい、先生には届かないだろう。
先生はメンスが渡したお金がわからず、 これが大気ならば観測者はある地点内部からくる光を見ることができない。
不透明なので観測できないといえる。
2. 伝達方程式の定量的思考

待望の伝達方程式です。
図は天文学および天体物理学序論、第4版(教保文庫)、p228の図です。
ここで考えるべきことは、光が通過した距離、そして消光の程度とガスを通過した後の光度変化がどうなるかです。
これは上で例えた教室の状況と同じです。
1) 光が通過した距離: 光が通過した角度が θなので、通過した距離は(dl/cosθ)となる。
2) 通過した光の光度変化量: 放出した程度 - 消光された程度
3) 上記の値は距離に比例する。
4) したがって、光の光度変化量 = (放出した程度 - 消光された程度) * 通過した距離上の式を以下の略号に置き換え、これを定量的な数式として立ててみましょう。
参考とすべきは 3での光学的深さは「波長」を基準に、伝達方程式では天文学および天体物理学で記述されているとおり「周波数」を基準に記述しているということです。
消光係数(χ): (不透明度*密度)と同じ値
放出係数(η) : ガスが放出する値
元亀関数(S=η/χ) : 光の放出量/光の吸収量
光学深さ(τ) : これが分からないなら、再度上に戻りましょう。
上の式は初めに書かれている定性的思考を数式に変えたものです。
ここに 光学的深さの微分量を両辺に割って、 μ=cosθと定義すると式は以下のように変わります。

これを積分因子を両辺に掛けて解を得たのが、天文学および天体物理学序論にある最後の数式です。

3. 結論 - 伝達方程式を理解する方法
1) 伝達方程式とは、天体内部で光がどのように伝達されるかを表しています。
2) 星の内部では光の消光と放出が同時に行われます。
3) したがって、伝達方程式は光の放出量から消光量を引き、それに光が通過した距離を掛けたものです。
実際、教職を準備する人々も伝達方程式を完全には理解しておらず、定性的に理解しているだけです。
繰り返し強調していますが、式を覚えるよりは理解することが重要です。
次の記事では、この伝達方程式が実際の惑星の大気でどのように使われるかについて学びたいと思います。







댓글을 불러오는 중...