ビリヤル定理について調べても正確に紹介されていないようで、この文を書いています。
おそらく教員採用試験を準備する人や科学高校の学生が読むことになるでしょう。
この記事を理解する前に、力学的エネルギーとポテンシャルエネルギー、そして円運動を物理的にどう記述するかを理解してから読み進めてください。
今回の文ではビリヤル定理について学び、次回の記事ではビリヤル定理を通じた銀河の質量推定について学びたいと思います。
1. ビリヤル定理
ビリヤル定理は乱雑に動く多数の粒子間の力について述べる定理です。
天文学でビリヤル定理を利用するのは、恒星や銀河の形成が1つの質点ではなく、不規則に動く多数の質点の集合で成り立つからです。

天文学でビリヤル定理は粒子の運動量と方向をすべて足した値です。
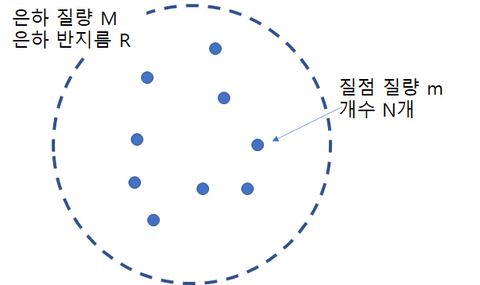
例えば上の図のように星が3つだけの銀河があります。
この銀河内で動いているすべての天体の運動量と方向の積を合計すればよいのです。この銀河でのビリヤル定理を求めるならば下のようになります。

上の値をそのまま見ると理解しにくいですが、時間に伴うビリヤル値の変化を見るとこれがどんな意味を持つのかが分かります。
そのためには運動量と方向の積を微分するとどんな意味を持つのかをまず知り、それを理解した上で先に進みましょう。以下のように数式を定義します。
物体の質量 = m, 速度 = v
加速度 = a, 運動量 = p = m * v
重力 = F
dp/dt(時間による運動量の変化) = ma = F距離と運動量の積を時間に関して微分すると以下の式が得られます。

ここで時間による運動量の変化は力であり、時間による距離の変化は速度なので、この式は以下のように変えられます。

最終的に運動量と方向の積を時間に関して微分すると、ある物体が持つ力学的エネルギーの合計が得られます。
同様にビリヤル値を時間に関して微分すると、ある系が持つ力学的エネルギーの合計が得られるのです。
その値は系が持つ位置エネルギーと運動エネルギーの2倍を合計したものと同じです。

上の銀河でビリヤル定理を行い、これを時間に従って微分すれば、星A、B、Cが持つ力学的エネルギーの合計が得られます。
銀河や星雲が安定し平衡を保っている状態であれば力学的エネルギーの変化はないはずです。
したがってビリヤル値の変化量も0でなければなりません。

力学的に安定し平衡を保っている銀河や星雲であれば、内部に存在する力学的エネルギーの総量は位置エネルギー総量の半分であるということです。
これを通じて、ある銀河やガス星雲の大きさと速度分散、温度のみを知っていれば質量が分かります。
2. 不安定な系でのビリヤル定理
系が安定していない状態ならばビリヤルは絶えず変化します。
ビリヤル値が減少するなら系は収縮し、増加するなら系は膨張します。
これを活用すれば、星が誕生する際に収縮可能な最大質量を求めることができます。

3. 高校物理で理解するビリヤル定理
では、高校のレベルでこの数式をどう簡単に理解できるか見てみましょう。
天体は互いに重力によって束縛されています。
ビリヤル定理は互いに束縛されているすべての天体の積分ですが、結局は1つの天体にある力学的エネルギーの合計と同じです。
したがって、1つの天体に対して力学的エネルギーがどのように求められるかを考えてみます。

上記のように地球周辺を公転する質量mの天体を仮定しました。
天体は地球を周回します。
このときの天体の力学的エネルギーは以下のとおりです。

このとき円運動の速度を求めてみましょう。
円運動は万有引力によって起こるため、向心力と万有引力は等しくなければなりません。
これを速度に関して整理すると

このような数式が得られます。
これを初めに記述した天体の力学エネルギーに当てはめてみましょう! すると....

上記のような結論になります。
結局、重力によって束縛された系では運動エネルギーの総和は位置エネルギーの半分になります。
これは上記のビリヤル定理を通じて得られた結論と同じです。

重要なのは、これを利用してどうやって天体の質量を推定できるかです。
これは次の投稿で扱います。
4. ビリヤル定理と放射放出
地球から非常に遠い天体が地球に接近し、最終的に地球に束縛された場合、系が持つエネルギーの総量はどうなるでしょうか?
最初に物体が静止状態だったと仮定すれば、系が持つエネルギーの総量は0だったでしょう。

しかし、この天体が重力によって引き寄せられ地球を周回するようになれば、位置エネルギーが減少し運動エネルギーに転換されるでしょう。

この場合、系が「安定した」状態だと仮定して力学的エネルギーの総量を求めると、驚くべきことに初めよりエネルギーが減少します。

束縛された天体のポテンシャルエネルギーの半分だけが消えたのです。
消えたエネルギーは熱に変換されます。
宇宙が真空状態であるため、伝導、対流を通してエネルギーが系に留まるためには損失はありません。
しかし放射はこれに対して自由なので宇宙空間に逃げることができます。
したがって、安定した系ならばこれだけのエネルギーは「放射放出」を通じて系を離れる必要があるという結論です。
5. 結論 : ビリヤル定理とは何か?
1) ビリヤル定理とは天体内部の質点の運動量と方向をすべて合わせた値です。
2) 時間に伴うビリヤル値の変化は天体の安定度を決定します。
3) 安定し平衡を保つ天体内でのビリヤル値の変化はなく、これを利用すれば天体の質量が推定できます。次回は3)を活用した天体の質量を推定する方法について説明しようと思います。引き続き記事を読みたい方は、以下のリンクにアクセスしてください。





댓글을 불러오는 중...