Hoy voy a intentar resolver el legendario problema relacionado con la esfera celeste de la Selectividad de 2018 para la materia de Ciencias de la Tierra 1, número 20, que recuerdo.
Actualmente, los problemas sobre la esfera celeste se han trasladado a Ciencias de la Tierra 2.
Si eres un estudiante que se prepara para el examen de Ciencias de la Tierra 2, puede ser bueno intentar resolverlo.
Por supuesto, si no estás preparando para la Universidad Nacional de Seúl, nadie tocará la materia de Ciencias 2....
Primero, vamos a revisar el problema con los ojos.
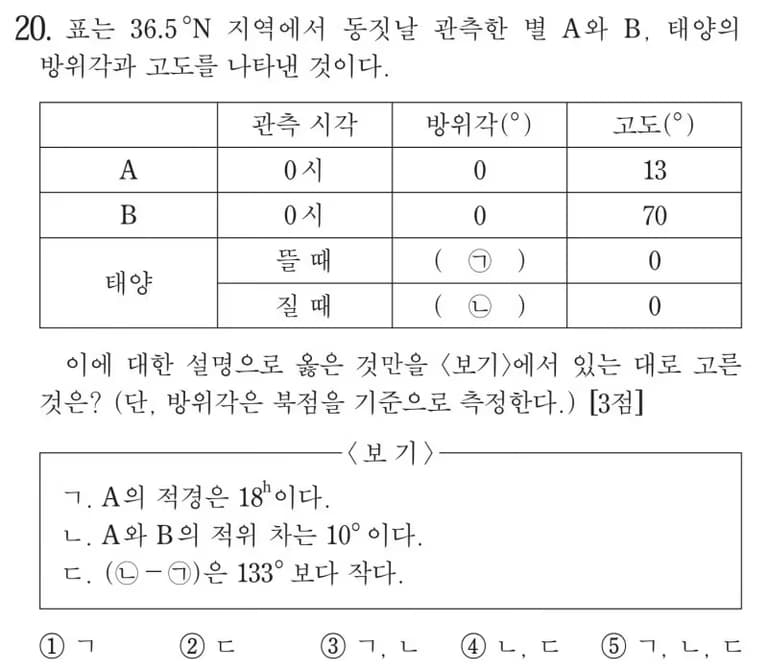
1. Problema número 20 de Ciencias de la Tierra 1 de la Selectividad 2018
2. Explicación de los puntos ㄱ y ㄴ
Ubicación de la observación: N 36.5 grados
Tiempo de observación de las estrellas A y B: 0 horas (medianoche)
1) Primero, dado que el área de observación está en 36.5º de latitud norte, el ángulo entre el horizonte y el polo norte celeste es de 36.5 grados.
2) Como la fecha de observación es durante el solsticio de invierno, la ascensión recta del sol es 18h y la declinación es -23.5º.
3) Como la hora de observación de las estrellas A y B es a las 0h, el sol estará en el lado opuesto al observador.
Como las altitudes de las estrellas A y B son 13º y 70º respectivamente, si se marcan en el polo norte celeste, se verían como sigue. Dado que es un poco confuso, borraré algunos elementos.

Ahora, si estimamos la ascensión recta y la declinación de cada estrella, podemos resolver los puntos ㄱ y ㄴ.
1) Como el acimut de las estrellas observadas a las 0h en el solsticio de invierno es 0, la ascensión recta de la estrella se obtiene en la intersección con el ecuador celestial a lo largo del meridiano. Al bajar por el meridiano, se puede ver que la ascensión recta de la estrella A es 18h y la de la estrella B es 6h.

2) La declinación se obtiene midiendo la distancia angular entre el polo norte celeste y cada estrella, y luego restando el valor de 90º. Debe ser fácil si se piensa usando la imagen anterior como referencia.
La altitud de la estrella A es 13º, por lo que 36.5º-13º=23.5º y 90º-23.5º=66.5º, así que la declinación de la estrella A es 66.5º.
La altitud de la estrella B es 70º, por lo que 70º-36.5º=33.5º y 90º-33.5º=56.5º, así que la declinación de la estrella B es 56.5º.3) Resultado
| Ascensión Recta | Declinación |
Estrella A | 18h | 66.5º |
Estrella B | 6h | 56.5º |

Por lo tanto, los puntos ㄱ y ㄴ del enunciado son correctos.
3. Explicación del punto ㄷ
Ahora vamos al esperado punto ㄷ. Estuve pensando por mucho tiempo al ver el punto ㄷ.
¿De dónde viene ese número 133º?
Vamos a dibujar las trayectorias del sol durante el solsticio de verano y el solsticio de invierno desde la latitud 36.5 grados.

Cuando el sol está en el equinoccio de primavera o de otoño, sale exactamente por el este y se pone exactamente por el oeste, por lo que la diferencia en los valores de acimut al salir y ponerse es de 180 grados.
Sin embargo, cuando el sol se mueve y tiene declinación, este valor cambia.
Actualmente, como el sol está en el solsticio de invierno, su declinación es -23.5º.
Por lo tanto, la diferencia en los valores de acimut al salir por el este y ponerse por el oeste será menor a 180.
Entonces, lo que nos intriga es cuánto varía el acimut. Vamos a ampliar el suelo del este.

Si ese valor es 23.5º, como hay una reducción del acimut tanto al este como al oeste, el valor de (㉡ - ㉠) sería 180 - 23.5º*2 = 133º.
Pero, dado que entendemos bien los triángulos gracias a los conocimientos del teorema de Pitágoras, sabemos que este valor debe ser mayor que 23.5º.
Por lo tanto, (㉡ - ㉠) debe ser menor a 133, por lo que el punto ㄷ es correcto.
4. Conclusión
Como los puntos ㄱ, ㄴ y ㄷ son todos correctos, la respuesta es 5.
Honestamente, este problema es demasiado difícil.
¿Habrá algún estudiante de tercer año de secundaria que pueda resolver esto....?
Parece ser un problema muy complicado.






댓글을 불러오는 중...