2018 College Scholastic Ability Test Earth Science 1 Question 20 Solution

Today, I'm going to tackle the legendary celestial sphere problem, question 20 from the 2018 Earth Science 1 CSAT.

Currently, problems related to the celestial sphere have moved to Earth Science 2.

It might be good practice for students preparing for Earth Science 2 in the CSAT.

Though unless you're aiming for Seoul National University, no one usually touches Science 2 subjects....

First, let's have a look at the problem.

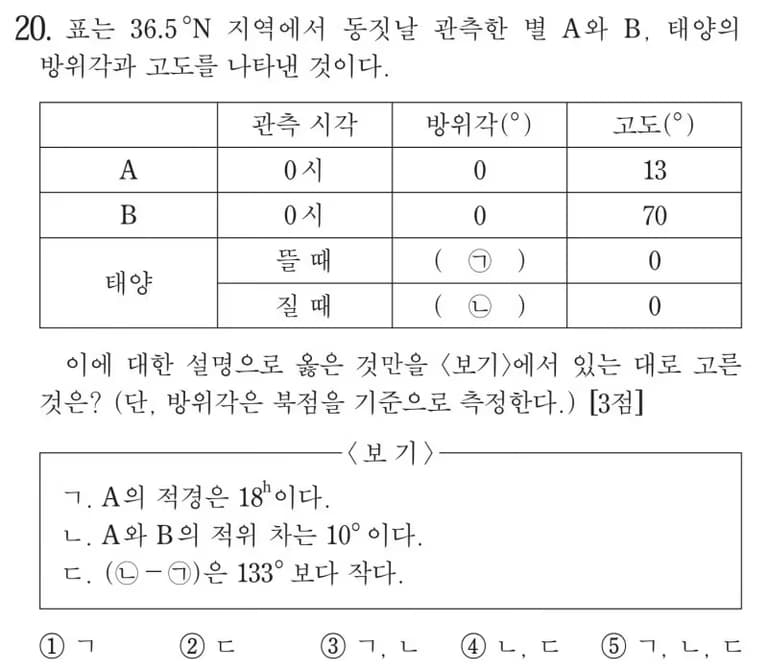
1. 2018 College Scholastic Ability Test Earth Science 1 Question 20

2. Solution for Viewpoints A and B

Observation location: N 36.5 degrees
Observation time for stars A and B: Midnight (00:00)

1) Since the observation location is 36.5º north latitude, the angle between the horizon and the celestial north pole is 36.5 degrees.
2) Since the observation date is the winter solstice, the Sun's right ascension is 18h, declination is -23.5º.
3) As stars A and B were observed at midnight, the Sun will be directly opposite the observer.

Since the altitudes of stars A and B are 13º and 70º respectively, representing these on the celestial north pole appears as shown. It might seem confusing, so let’s remove some elements.

Now, by estimating the right ascension and declination of each star, you can solve viewpoints A and B.

1) Since the azimuth angle of stars observed at midnight on the winter solstice is 0, the right ascension can be found where the celestial equator meets the meridian. Going down along the meridian, star A’s right ascension is 18h, and star B’s is 6h.

2) To find declination, measure the angular distance from the celestial north pole to each star, then subtract from 90º. Refer to the above diagram for ease.

Star A's altitude is 13º, so 36.5º-13º=23.5º and 90º-23.5º=66.5º, thus Star A's declination is 66.5º.
Star B's altitude is 70º, so 70º-36.5º=33.5º and 90º-33.5º=56.5º, thus Star B's declination is 56.5º.

 3) Result

Therefore, both viewpoints A and B are correct.

3. Solution for Viewpoint C

Now, the highlight: viewpoint C. I pondered a lot over viewpoint C.

Where on earth did the number 133º come from?

Let's draw the Sun's movement path for latitude 36.5 degrees during the summer and winter solstices.

When the Sun is at an equinox, it rises due east and sets due west, making the azimuth angle difference at sunrise and sunset 180 degrees.

However, as the Sun moves and declination occurs, this value changes.

Currently at the winter solstice, the Sun's declination is -23.5º.

Thus, the azimuth angle difference from east to west is less than 180.

Now the question is, by how much do they differ? Let’s zoom in on the eastern horizon.

If that value is 23.5º, then the reduction in azimuth angle occurs on both east and west, making the value of (㉡ - ㉠) = 180 - 23.5º*2 = 133º.

But, given our understanding of triangles from Pythagoras, we know this value must be greater than 23.5º.

Hence, (㉡ - ㉠) must be less than 133, making viewpoint C correct.

4. Conclusion

Since viewpoints A, B, and C are all correct, the answer is choice 5.

Honestly, this question is quite petty.

I wonder if any high school seniors solved this....

It seems like a killer problem.